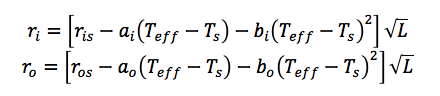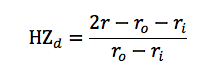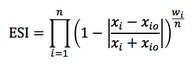UPDATE: ve zdroji výpočtu došlo ke změně vzorce, článek jsme proto aktualizovali.
Obyvatelná oblast (HZ) se stala termínem, který někteří hltají asi stejně rychle a vášnivě, jako ke konci minulého století hltali zmínky o vodě v jakémkoliv skupenství a podobě kdekoliv ve Sluneční soustavě. Mít kamennou planetu o hmotnosti Země (plus mínus), která obíhá okolo své hvězdy v HZ, znamená, že na povrchu takovéto planety čistě teoreticky může být voda v kapalném skupenství. Zmínit se o exoplanetě v obyvatelné oblasti je sice možná dobré na upoutání pozornosti zívající mladé slečny během přednášky ale to je tak asi vše, neboť….
HZ může být určitou základní pomůckou pro orientaci v exoplanetární džungli a to zejména pro léta následující, kdy nám budou objevy exoplanet padat do klína (nebo v to aspoň doufáme). Ve skutečnosti nám však HZ nic o obyvatelnosti planety neřekne….ani nemůže, při narození nedostala do vínku dostatečnou výbavičku. HZ vychází pouze z parametru mateřské hvězdy (konkrétně její zářivosti) a vzdálenosti planety od hvězdy. Jenomže vesmír není tak jednoduchý. Klima a teplotu na povrchu planety či exoměsíce ovlivňuje také atmosféra, o které zejména u kamenných exoplanet nevíme zhola nic a při výpočtu parametrů HZ ji tak trochu ignorujeme. Díky tomu se astronomové dostávají do trochu bizarní situace, kdy v datech hledají planetu, na jejímž povrchu bude tzv. rovnovážná teplota bod bodem mrazu nebo lehce nad ním. Ne, že by snad byli lovci exoplanet náruživí fanoušci zimním sportů, ale třeba atmosféra Země ohřívá povrch planety o 30 °C. V případě Venuše je to ale rovných 500 °C!
Kromě toho zde máme samozřejmě i filozoficko-astrobiologické úvahy o tom, zda je voda opravdu tak důležitá a mimozemské breberky nemohou vegetovat i v jiném rozpouštědle nebo zda blízkost k hvězdě nelze nahradit jiným zdrojem tepla, což může být aktuální třeba u exoměsíců. Konec konců stále a pořád hledáme život po měsících Jupiteru a Saturnu, na hony vzdálených od obyvatelné zóny okolo Slunce.
Vypočítat parametry HZ lze několika způsoby, které jsou ale obvykle principiálně stejné. Střed HZ je druhá odmocnina zářivosti hvězdy. Okolo tohoto středu si pak můžete vystavět mantinely (vnější a vnitřní okraj HZ). Obecně můžeme říci, že čím je hvězda hmotnější, tím je vzdálenost mantinelů větší. Například u chladných červených trpaslíků může být hranice v řádu setin astronomických jednotek, u hvězd hmotnějších než Slunce to jsou desetiny.
Samozřejmě i pro okraje HZ jsou vzorečky, kdy se zářivost ještě před odmocněním podělí parametry pro určité typy hvězd. O těchto výpočtech jsme už psali ve dvou článcích, ve kterých se dozvíte i to, jak vypočítat zářivost hvězdy na základě její velikosti a teploty:
Pamatovat si však, kde HZ pro danou hvězdu končí a kde začíná, je docela nepraktické. Před časem se ale objevil návrh nového postupu výpočtu HZ, který jde na celou věc trochu jinak.
Odvození výpočtu najdete v odkaze a zde:
Teff – je povrchová teplota mateřské hvězdy (v Kelvinech)
L je zářivost mateřské hvězdy (v násobcích Slunce)
r0 je vnější a ri vnitřní hranice HZ
Ostatní jsou konstanty: Ts = 5700 K, ai = 2,7619.10-5, bi = 3,8095.10-9, ao = 1,3786.10-4, bo = 1,4286,10-9, ris = 0,72 a ros = 1,77
Konečný vzorec pak je:
, kde r je vzdálenost planety od hvězdy (v AU) a Hzd je vzdálenost HZ v jednotkách HZU.
Výpočet je to samozřejmě poměrně složitý a proto nabízíme pomůcku. Stačí když si stáhnete soubor pro MS Excel a do políček doplníte L, Teff a r.
Stejný soubor nabízíme i pro volně šířitelný program OpenOffice Calc – vypocet.
0 je střed obyvatelné oblasti
1 je vnější okraj obyvatelné oblasti
-1 je vnitřní okraj obyvatelné oblasti.
Obyvatelná oblast tak leží mezi hodnotami -1 a 1.
Příklady HZU pro některé známé (exo)planety:
- Země = -0,5 HZU
- Venuše = -1 HZU
- Gliese 581 d = +0,78 HZU
Je dobré poznamenat, že tento nový způsob je v podstatě tím starým v novém balení. Ani tento výpočet nám o obyvatelnosti planety neřekne více nebo méně a také nebere v úvahu výstřednost dráhy – exoplaneta se totiž může pohybovat po eliptické dráze, kdy jen malou část jednoho oběhu stráví v HZ.
Všimněte si, že pro Zemi nevychází hodnota jako 0 ale jako -0,78, to naznačuje, že výsledky je nutné jednak brát s rezervou a potom, že i v tomto případě tak trochu platí pravidlo „ano / ne“. Pokud dráha planety leží v intervalu HZU -1,1 je v HZ, pokud leží mimo, pak v HZ samozřejmě není. Tento výpočet se tak spíše hodí pro porovnávání planet a jejich vzdálenosti od HZ.
Jak moc jsi, krásko, podobná Zemi?
Abychom mohli planety lépe porovnávat, přišli někteří autoři s jiným postupem. Pod zkratkou ESI (Earth Similarity Index) se ukrývá Index podobnosti se Zemí. Pokud má planeta ESI rovný číslu 1, pak je zcela podobná naší planetě jako vejce vejci ale pouze na základě předem daných kritérií. Čím více se pak hodnota blíží k nule, tím je planeta od naší rodné hroudy co do podobnosti vzdálenější. Například pro Mars je ESI 0,697, pro Jupiter 0,338 a třeba exoplaneta Gliese 581 d má hodnotu 0,739.
Výpočet ESI vychází ze čtyř základních parametrů:
Poloměru
Hustoty
Povrchové teploty
Všimněte si, že mezi čtyřmi parametry není údaj o vzdálenosti či oběžné době. Ten je totiž ukryt právě v parametru „povrchová teplota“. Jak ale autor došel k odhadu povrchové teploty v případě exoplanet, je mi trochu záhadou. Rovnovážnou teplotu určit můžeme, ale ta samozřejmě nebere v úvahu vliv atmosféry. Stejně tak poloměr planety v případě, že nevykonává tranzity, bude asi spíše hrubým odhadem.
ESI pak vypočítáme dle vztahu:
, kde xi je parametr pro danou planetu, xi0 je parametr pro Zemi, wi je tzv. váhový exponent a n je počet parametrů.
Pro jednodušší orientaci zavádí autor celkem tři ESI indexy:
- ESIi je vnitřní index, který v sobě zahrnuje údaje o poloměru a hustotě planety.
- ESIs je povrchový index, obsahující únikovou rychlost a povrchovou teplotu.
- ESIg je globální index, který zahrnuje všechny čtyři parametry (povrchovou teplotu, poloměr, hustotu, únikovou rychlost). Dle libosti může být rozšířen o další parametry.
Váhové exponenty a referenční hodnoty
Příklad:
Jako příklad si zvolme Mars a index ESIi. Potřebovat budeme údaje o poloměru a hustotě Marsu a to v násobcích Země:
- Poloměr Marsu: xi = 0,53 Země
- Hustota Marsu: xi = 0,71 Země
Z tabulky si vezmeme váhové exponenty. Pro poloměr je 0,57, pro hustotu 1,07.
Údaje bereme vzhledem k referenční hodnotě Země (1), takže xi0 = 1.
Parametry máme dva, takže n = 2
Hodnoty dosadíme do vzorce pro každý parametr zvlášť a oba výsledky mezi sebou vynásobíme. Měl by nám vyjít ESIi = 0,815.
Pokud si nevíte rady, tak polopaticky:
Pro poloměr:
(0,53 – 1) / (0,53 + 1) = -0,307189542 (údaj je v absolutní hodnotě, takže minusové znaménku si můžeme odmyslet)
1 – 0,307189542 = 0,692810457
Exponent wi / n = 0,57 / 2 = 0,285
0,692810457 umocníme na 0,285 = 0,900689528
Analogicky provedeme výpočet pro hustotu, kde nám hodnota vyjde 0,905360088
Oba výsledky vynásobíme a dostaneme ESIi = 0,815
Pokud budete počítat globální index ESIg, bere v potaz 4 parametry a n = 4
Tabulky:
Zdroje: